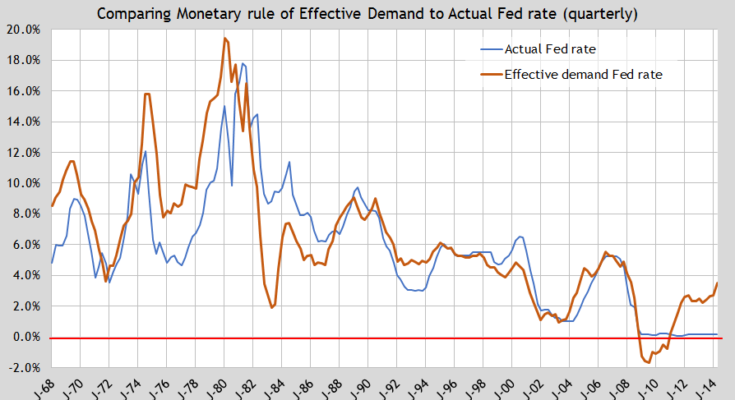
We see more talk now about how the Fed may have to raise its base overnight rate (Fed funds rate) faster than planned. Data is coming out that points to a need to raise the Fed funds rate.
Last week I posted this graph showing the Fed funds rate in comparison to the “Effective Demand†rule I developed for determining the base nominal rate for any central bank. (link) My ED rule has trended very well with the actual Fed funds rate over time.

Just recently at the right (2nd quarter 2014) we see that the ED rule is calling for a quick rise in the Fed rate. It may be a blip that will correct downward in the next quarter, but maybe not. CPI inflation (less food & energy) jumped up in the 2ndQ-2014. Was it a blip? We will watch core CPI over the next few months to know.
The ED rule I use does not estimate “potentialâ€, like the Taylor rule which depends on an estimate of potential GDP or potential unemployment (NAIRU). The ED rule I developed uses real data… With only capacity utilization, unemployment, labor share and a natural real rate, I match the Taylor rule. I don’t even estimate a NAIRU in my rule.
Part of my ED rule in blue. The corresponding portion of the Taylor rule in red.
z*(TFUR2 + LSA2) – (1 – z)*(TFUR + LSA) = NR + a*(y – y*)
z = (2*LSA + NR)/(2*(LSA2Â + LSA))
TFUR = Total Factor Utilization Rate, (capacity utilization * (1 – unemployment rate))
LSAÂ = Labor Share Anchor which stays fairly stable throughout a business cycle.
NRÂ = Natural real rate of interest
a = Estimated coefficient from Taylor rule for estimating slack in “potentialâ€. Debate exists over correct value.
y = Real GDP for Taylor rule.
y* = “Potential†Real GDP for Taylor rule.
The corresponding portion of my ED rule (blue) does not have the problems trying to estimate “potential†GDP nor even the correct value for the “a†coefficient. Paul Krugman and John Taylor, for example, do not agree on the value of “aâ€. My ED rule has no room for such a debate as there are no coefficients which are statistically obtained. You just get the data and arrive at the Fed funds rate.